Anagrams and (brains vs. cpu)

In AI there is a vast category of algorithms which follow a (blind) generate and test strategy. They essentially "generate" the solutions (as a whole or step by step) and then test if the solution complies with an acceptance function. Unfortunately, this simple strategy is usually ineffective. The cost is often exponential in the size of the input and since there is no "intelligence" all solutions (even dumb ones) are explored). In AI it is customary to use smarter search techniques (A*) or to "change" the problem so that even smarter solutions are viable. An apparently unrelated example, is "finding the anagrams of a word". The trivial (and generate and test) solution is:

1. [generate]: try all the permutations of the word
2. [test]: check if the word is in the dictionary

and this strategy also shares the very same problems of the other generate and test strategies. All the permutation of a k characters word are k! = k(k-1)(k-1)...2. It is customary to see algorithms like:

def yield_anagrams(dictionary, word):
return [word for word in
(''.join(candidate) for candidate in it.permutations(word))
if word in dictionary]

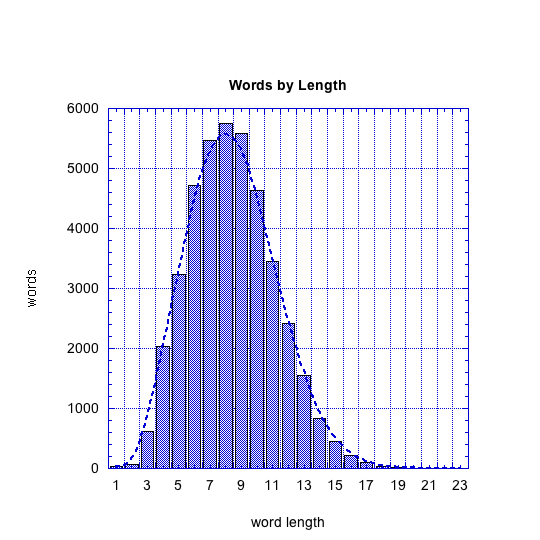
which in other languages are even longer and less attractive. This approach is rather tempting for very small words. I got some interesting wordlists from here. As a good starting point I used the 12Dict list and in particular the 2of12.txt file. More info on the lists can be found in the ReadMes. In the rest of the post we are going to work with that dictionary. 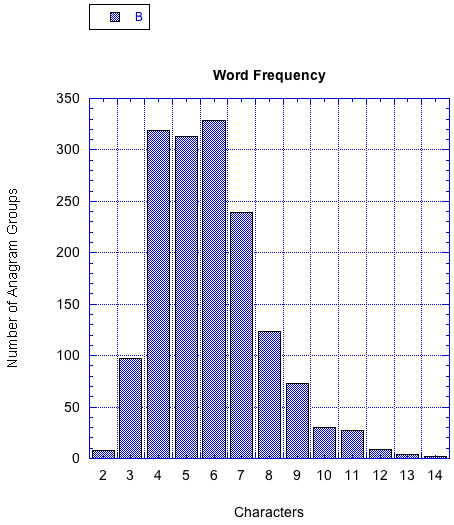This graph shows the distribution of word lengths: This other graph shows how many groups of words with the same anagram we have by word length: For those preferring tabular data:

Size of the word	Number of groups
2	8
3	97
4	319
5	313
6	329
7	239
8	124
9	73
10	30
11	27
12	9
13	4
14	2

As we can see, the longest words with anagrams are 14 characters long. Even though most anagrams are very short word, our algorithm should work reasonably well with every input. The code I showed cannot. For example, let us consider the time required to compute the anagrams of words of increasing size:

scoreless	9	0,174
praetorian	10	1,828
rationalize	11	21,03
indiscreetly	12	269,0

In the first graph, we both axes are linear. If we do not believe me when I say that the growth is exponential, then look at this other graph: here the y axis is in logarithmic scale. Exponential means that if you simply change the implementation or the implementation language, things are going to blow up once again a couple of steps later. So, let us sum up: we have 41238 words. Of these words, 5644 have 12 or more characters. If we suppose that anagrams for words longer than 12 character cost exactly as anagrams for words 12 characters long, the whole process is going to take 1518236 seconds, that is to say more than 17 days. In fact, the whole process is going to be far more expensive. I have a full table (excel -- here you may want to download the file --, csv) with times estimated using the formula derived from our 4 values. Of course, this is not extremely precise, but the sheer magnitude of the computed values should make the point clear. To compute all the anagrams for all the words up to size 11 (included) it takes one day. If you want to reach size 13 it is going to take one year. However, it is still a long way to process all the words... for example, in order to discover that our dictionary words with anagrams of length 15, our program is going to run for more than 38 years. The conclusion that no words longer than 14 has an anagram (according to our dictionary) takes more than 4000000 years. Of course, I did not wait all that time to gather these results... tomorrow I am showing a smarter strategy which drops the required time from 4000000 years to 0.16 seconds.

Technorati Tags: Efficiency, Optimization, Python, Algorithms, Anagram